Надо ли пенсионерам заново идти в школу!

Почему зеленое яблоко -не красное?!
При подготовки статьи о букве «Ф» (https://45-90.ru/discussions/893-bukva-f-kak-kamen-pretknovenija-v-173-fz-rf-o-trudovyh-pensijah.html) пришлось столкнуться не только с проблемой касательно этой буквы. Вопрос стоял еще жёстче - "Сама формула математически не правильная, вернее смысл заложенный в ней законодателем, не совпадает с математическим правилом вычисления".
Мой оппонент, с которого и начался весь этот сыр-бор, утверждает, что
СК х ЗР/ЗП х СЗП = СК х ЗР/(ЗП х СЗП )
а все из за того, что в одном из энциклопедических справочников в качестве примера деления дробей была приведена такая запись
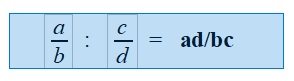
мои пояснения, что такая запись неправильная, и что это тоже или опечатка или описка, опять «уперлись» в глухую стену.
Кто учился в 3 классе начальной школы и не прогуливал математику, прекрасно помнят порядок математических действий. Порядок выполняется слева направо, с начало умножение или деление, затем сложение или вычитание, если скобки есть, то сначала вычисляем все что в скобках, затем опять слева направо, если внутри скобок есть еще скобки, то сначала, самые внутренние скобки.
Поэтому правильная запись будет такой
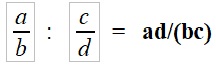
и никак иначе., что и отмечено в БРЭ и других математических справочниках.
На моё предложение оппоненту доказать, что
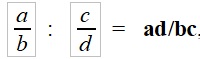
он привел очень простое доказательство раз у выражений

одна сторона равна , значит и вторая сторона тоже равна, то есть если
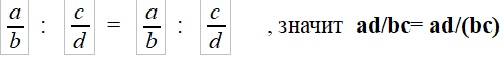
Вот видите какое простое доказательство!))
То есть вот вы дали двум разным людям два одинаковых яблока красного цвета, но один говорит, что яблоко красное, а другой, что яблоко зеленое, вывод напрашивается только один, что зеленый цвет = красный цвет. То что один из этих людей может просто ошибается с умыслом или действительно так видит в расчет не берется.
На самом деле доказательство не такое уж сложное. И оно основано, на определении самого деления и порядка математических действий. То есть любое деление можно представить в виде произведения, в котором делитель "преображается" в сомножитель, но только в степени -1.

теперь такие же преобразование проведем с ad/bc и ad/(bc)
2 ) ad/bc = a x d / b x c = a х d x b-1 х c
ad/(bc) = a x d / (b x c) = a х d x (bхc)-1 = a х d x b-1 х c-1
где х — знак умножения
а теперь посмотрите какое полученное выражение во втором преобразовании равно полученному выражению из первого преобразования.
Поэтому пенсы, кто с математикой не в ладах, не закидывайте суды исками о неправильной формуле , все в ней правильно! И в скобки ЗР/ЗП брать не обязательно (свойство деления произведения двух натуральных чисел на натуральное число), от этого результат не изменится.


Ранее я предупреждал, что бухгалтер (являющийся сотрудником ПФ/СФ), предполагающий (без всяких на то оснований), что в энциклопедическом издании, неоднократно переиздававшемся и являющемся национальным достоянием, (цитирую): "..., что такая запись неправильная, и что это тоже или опечатка или описка" (конец цитаты) является САМО ошибкой природы (опечаткой), ну, потому, что если запись из энциклопедии есть опечатка (может же это существо так предполагать?), то — и я могу предполагать ЛЮБОЙ бред, отменяющий существование этого существа.
Привожу (для заинтересованных граждан) расширенное (и окончательное) доказательство того, что
(a/b): (c/d ) = ad/bc:
https://disk.yandex.ru/i/oqUu1XJpDPs23w
По приведенной ссылке можно ознакомиться с простейшим текстом, где приводятся (мною — bb) известные (и доказанные неопровержимо) с древнейших времён правила выполнения тождественных преобразований, в соответствии с которыми именно однозначно и неопровержимо запись выражения вида ad/bc тождественна записи ad/(bc), потому что знаменатель «bc» (будь он со скобками или без оных — он всё равно знаменатель по определению!) не может обращаться в нуль. Ну, потому что «b» — это сомножитель из знаменателя получаемой (по неопровержимому определению о делении дробей, которое является законом природы и не может быть опровергнуто! Это определение для того и написано, чтобы никто его даже не пытался опровергнуть) итоговой (ad/bc) дроби, а "c" — это т а к о й же сомножитель из того же знаменателя:
ad/bc = (a/b): (c/d ) = ad/bc
и
ad/(bc) = (a/b): (c/d ) = ad/(bc),
откуда следует, что (да, так доказал Аристотель: равенство исходных записей тождественно означает равенство конечных записей! Если 2 х 2 = 4, а 1 + 1 + 1 + 1 + 1 = 4, то 1 + 1 + 1 + 1 = 2 х 2. Прошу не сходить с ума и не предполагать, что Аристотель — идиот. Верно обратное: что идиотом является тот, кто посмеет предположить, что Аристотель о п е ч а т а л с я):
ad/bc = ad/(bc).
А приведенная запись (цитирую):
"ad/bc = a x d / b x c = a х d x b-1 х c" (конец цитаты)
— является именно тем самым «красным яблоком» (брехнёй, высосанной из пальца) — потому что сомножитель «c» (в таком виде могущий обратиться в нуль! — беда тут), стоящий в знаменателе по определению (!), что доказано выше, ДОЛЖЕН иметь не такой вид «c», а именно вид «c-1 » (ну, потому что такая, приведенная в цитатке запись, не соответствует определению о делении дробей, то есть, противоречит ему, и не является тождественной исходной записи «ad/bc»), из которого следует, что
c-1 ≠ 0.
В смысле: надо же (уже. Скока можна на второй год оставаца?!) переходить из третьего (где граждане, до сих пор пребывающие ТАМ, не имеют понятия о знаменателе) класса хотя бы в восьмой (ётм).
В смысле: тот, кто отказывается признавать (и исполнять) общественное (по приведенной ссылке) соглашение о том, что на «нуль делить нельзя» (и взаимосвязанные с этим правилом иные правила выполнения тождественных преобразований) — впредь освобождён от обсуждений своих (таких) бредовых текстов (то есть, вначале обязан известить, что: именно признаёт и будет исполнять).
bb
27.03.2023г.
Даааа… умеете вы растекаться мыслью по дереву!)))
я же вам не зря говорила, учите порядок математических действий. Там все просто и понятно.
для наглядности приведу два примера. А вы мне напишите пожалуйста как вы их решили и какой получился у вас результат.
9:3*3 =
9:3^2 =
где 3^2 это три в квадрате.
Кстати, то что вычисления значений степени, корня, логарифма и других функций, выполняются до выполнения остальных действий, то есть считают, что они заключены в скобки, изучают в старших классах. Поэтому я допускаю, что вы этого можете не знать, поэтому и привели в пример формулу (в своем соглашении), в таком виде, в котором она нигде не приводится.
Вот вам пример из того же СЭС, на который вы так любите ссылаться, везде все что стоит за косой чертой, стоит в степени (где есть одинаковые сомножители) и оййй там еще и делитель (знаменатель) взят в скобки везде где есть несколько сомножителей, интересно почему?)))))
п.с… То что много опечаток в разного рода словарях/справочниках/энциклопедиях ни для кого не секрет, человеческий фактор. Вот недавно старшеклассник нашел ошибку в орфографическом словаре (https://deti.mail.ru/news/v-saranske-podrostok-nas... !))
Или вот например в справочнике Выгодского по элементарной математике опечатка. Все можно сказать свершившейся факт, но те кто с головой дружит, спокойно применяют такую математическую операцию как умножение.
Кстати. у меня внучатый племянник получил пятерку по математике, потому что нашел в учебнике за 7 класс опечатку и именно вот по такому же случаю. На одной из страниц в примере при переходе с горизонтальной дробной черты на знак":" знаменатель был взят в скобки и поэтому порядок действий не изменился, а на другой странице в точно таком же примере скобка отсутствовала и результат вычисления изменился, потому что изменился порядок действий.
Ну и напоследок про тождество. Я с вами абсолютно согласна, что если А=В и А=С, то и В=С, это правильная логическая цепочка, но какое она имеет отношение к нашей формуле? Ведь вы так и не смогли доказать, что А=В, поэтому о тождестве тут речь вообще не идет.
Вот это прямо можете наизусть заучить, очень показательно и верно!):
Ну и напоследок 2: Запомните, что двоеточие (:), косая черточка (/), горизонтальная дробная черта (-) это всё знак деления, а не знак дроби!)
Засим откланиваюсь.
А — нельзя ли получить «задание» на решение примерчиков в виде с горизонтальной чертой дроби?
То есть, прошу привести чёткое словесное правило (в сочетании с математической записью-примером: как применять такое правило, с указанием источника, естественно), в соответствии с которым следует выполнить поиск знаменателя и — затем, после установления его состава и определения ОДЗ (нельзя же на нуль делить!), - выполнить именно тождественное преобразование исходного примерчика к виду с горизонтальной чертой дроби (ну, так, ведь, следует поступать в третьем классе, когда понятия о слове «знаменатель» нет ни у кого, даже у самого крутого отличника).